- Instrument
- SHINE Spectro-Gonio bidirectional reflection Vis-NIR
- Spectral observation mode
- spectrum
- Valid spectral range(s)
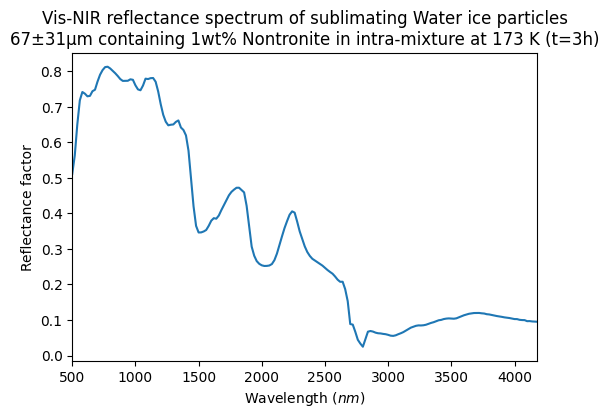
- 500.0 - 660.0 $nm$ ; 680.0 - 1380.0 $nm$ ; 1400.0 - 2980.0 $nm$ ; 3000.0 - 4180.0 $nm$
- Observation geometry
- bidirectional : i=0.0° ; e=30.0° ; az=0.0° ; ph=30.0°
- Angle observation mode
- fixed angles
- Spatial observation mode
- single spot
- Name
- Sublimation residue made of Nontronite on Water ice particles 67±31μm containing 1wt% Nontronite in intra-mixture at 173 K
- Origin
- natural terrestrial
- Texture
- other, loose granular
- Thickness
- 20.0 $\pm$ 1.0 $mm$
- Temperature
- 173.0 $K$
- Pressure
- 1.5e-06 $mbar$
- Irradiated by
-
- None
References
- Data reference
- Schroeder, Stefan; Poch, Olivier; Ferrari, Marco; DeAngelis, Simone (2019): Vis-NIR reflectance spectra of Nontronite NAu-1, pure, mixed with Water ice, during and after ice sublimation. SSHADE/CSS (OSUG Data Center). Dataset/Spectral Data. https://doi.org/10.26302/SSHADE/EXPERIMENT_OP_20200701_001
- Publications